RESEARCH ARTICLE
Kinetic and thermodynamic compensation of non-enzymatic browning of clarified lemon juices
Compensación cinética y termodinámica del pardeamiento no enzimático de zumos clarificados de limón
Raquel Ibarz1 * ; Alfonso Garvín1 ; Oriol Tomasa1 ; Albert Ibarz1
1 Departamento de Tecnología, Ingeniería y Ciencia de Alimentos. Universitat de Lleida. Av. Rovira Roure, 191, 25198, Lleida, Catalunya. España.
* Corresponding author: raquel.ibarz@udl.cat (R. Ibarz).
Received: 31 December 2023. Accepted: 1 May 2024. Published: 13 May 2024.
Abstract
This paper presents a study on kinetic and thermodynamic compensation to evaluate the kinetics of non-enzymatic browning of clarified lemon juices. In a previous work, the kinetic constants of browning were presented using the evolution of the absorbance at 420 nm (A420) and luminosity (L*) for different soluble solids contents (64.6; 50; 35; 20 and 10 ºBrix) and different working temperatures (70, 80, 90 and 95 ºC). The parameters of the Arrhenius equation were obtained by fitting the kinetic constants and temperatures. The variation of lnK0 with Ea follows a linear trend, so there is kinetic compensation, with isokinetic temperature values being 126.6 ºC and 149.7 ºC for A420 and L*, respectively. The transition state equilibrium constants were determined using the Eyring equation for each soluble solids content and each temperature. The equilibrium constants were adjusted to the Van't Hoff equation and the set of pairs of estimated values for the activation enthalpy and the activation entropy also followed a straight line, which causes thermodynamic compensation, with isoequilibrium temperatures of 112.8 ºC and 136.3 ºC for A420 and L*, respectively. It was concluded that the browning mechanism is the same for the ranges of soluble solids content and temperature studied. Since all isokinetic and isoequilibrium temperatures were higher than the working temperature values, it was also concluded that the control was enthalpic for all cases. To avoid the deterioration of these juices, it is advisable to intervene in the working temperature, trying to ensure that the heat treatment is carried out at the lowest possible temperature.
Keywords: kinetic compensation; thermodynamic compensation; non-enzymatic browning; kinetic constants; isokinetic temperature; isoequilibrium temperature.
Resumen
En este artículo se presenta un estudio sobre la compensación cinética y termodinámica para evaluar las cinéticas de pardeamiento no enzimático de zumos clarificados de limón. En un trabajo anterior se presentaron las constantes cinéticas de pardeamiento utilizando la evolución de la absorbancia a 420 nm (A420) y luminosidad (L*) para distintos contenidos en sólidos solubles (64,6; 50; 35; 20 y 10 ºBrix) y diferentes temperaturas de trabajo (70, 80, 90 y 95 ºC). Los parámetros de la ecuación de Arrhenius se obtuvieron al ajustar la variación de las constantes cinéticas con la temperatura. La variación de lnK0 con Ea sigue una tendencia lineal, por lo que existe una compensación cinética, con valores de la temperatura isocinética de 126,6ºC y 149,7ºC para A420 y L*, respectivamente. Las constantes de equilibrio del estado de transición se determinaron utilizando la ecuación de Eyring para cada contenido en sólidos solubles y cada temperatura. Las constantes de equilibrio se ajustaron a la ecuación de Van't Hoff y el conjunto de los pares de valores estimados para la entalpía de activación y la entropía de activación siguieron una línea recta lo que da lugar a la compensación termodinámica, con unas temperaturas de isoequilibrio de 112,8 ºC y 136,3 ºC para la absorbancia a A420 y L*, respectivamente. Se concluyó que el mecanismo de pardeamiento es el mismo para los intervalos de contenido en sólidos solubles y temperatura estudiados. Dado que todas las temperaturas isocinéticas y de isoequilibrio fueron superiores a los valores de las temperaturas de trabajo, también se concluyó que el control fue entálpico para todos los casos. Para evitar el deterioro de estos zumos se aconseja intervenir en la temperatura de trabajo, intentando que el tratamiento térmico se lleve a cabo a la menor temperatura posible.
Palabras clave: compensación cinética; compensación termodinámica; pardeamiento no enzimático; constantes cinéticas; temperatura isocinética; temperatura de isoequilibrio.
DOI: https://doi.org/10.17268/sci.agropecu.2024.020
Cite this article:
Ibarz, R., Garvín, A., Tomasa, O., & Ibarz, A. (2024). Compensación cinética y termodinámica del pardeamiento no enzimático de zumos clarificados de limón. Scientia Agropecuaria, 15(2), 269-277.
1. Introducción
Los procesos de elaboración de zumos clarificados de frutas incluyen diferentes operaciones unitarias en las que los zumos experimentan cambios en su contenido en sólidos solubles. Además, durante el procesado se ven sometidos a diferentes temperaturas, algunas de ellas elevadas, como en la etapa de concentración por evaporación. Todo ello suele incidir negativamente en las propiedades del zumo, tanto desde el punto de vista nutricional como organoléptico. Uno de los deterioros más comunes que experimentan los zumos es el pardeamiento no enzimático debido a la reacción de Maillard entre azúcares reductores y los grupos amino libres (Cornwell & Wrolstad, 1981; Waller & Feather, 1983; Manayay & Ibarz, 2010; Ibarz 2010; Echavarría et al., 2016). Según sea el contenido en sólidos solubles del zumo, el grado e intensidad del pardeamiento no enzimático varía, siendo más pronunciado cuanto mayor es su concentración (Beveridge & Harrison, 1984). Generalmente, las industrias que procesan zumos de limón suelen concentrarlos hasta un contenido en sólidos solubles de aproximadamente 65 ºBrix, por lo que, una vez obtenido el producto final concentrado, se almacena a bajas temperaturas de alrededor de 5 ºC.
Existen diferentes métodos para estudiar y evaluar los procesos de deterioro de los zumos. Uno muy sencillo es determinar cómo evolucionan con el tiempo diferentes parámetros colorimétricos, como la absorbancia que los zumos presentan a una longitud de onda de 420 nm o bien los valores de coordenadas CIELab. Los zumos con diferente contenido en sólidos solubles se someten a diferentes temperaturas y se evalúan los parámetros colorimétricos a diferentes tiempos. La variación de estos parámetros con el tiempo permite obtener las constantes cinéticas del proceso de pardeamiento y con ello poder predecir cómo evolucionará el color de un zumo de cierta concentración en sólidos solubles para una determinada temperatura (Toribio & Lozano, 1986; Ibarz et al., 2023).
1.1. Compensación cinética y termodinámica
Las compensaciones cinética y termodinámica se han aplicado en diversos procesos químicos, físicos, biológicos y alimentarios (Beristain et al., 2010; Aguilar et al., 2016; Garvín et al., 2019; Özilgen, & Bayindirli, 1992; Ibarz et al., 2017; Salinas et al., 2019, 2021). En La literatura reciente se pueden encontrar trabajos que aplican la compensación cinética en áreas no alimentarias. Así, Hotta & Koga (2024) lo aplican al estudio de la descomposición térmica reversible de CaCO3 en estado sólido, lo que les permite verificar que se cumple la compensación cinética y obtener los puntos isocinéticos. La pirolisis es una tecnología ampliamente utilizada para convertir la biomasa en biocombustibles en estado líquido o gaseoso (Jankovic et al, 2023; Wang et al., 2024), aunque en estos procesos se utilizan temperaturas sumamente superiores a las utilizadas en los procesos alimentarios convencionales. En el primero de estos dos últimos trabajos se examina la descomposición pirolítica de compuestos lignocelulósicos (Miscanthus gigantescus y Arundo donax L.), obteniendo que se cumple tanto la compensación cinética como termodinámica y pueden determinar que el alcance del efecto de la compensación depende de la composición de cada muestra; además, se pone de manifiesto que existe al menos tres tipos de mecanismos cinéticos. En el trabajo de Wang et al. (2024) se estudia la pirólisis de la microalga Chlorella pyrenoidosa utilizando la compensación cinética para poder caracterizar de forma adecuada la cinética tan compleja de este proceso térmico. En el trabajo de Lyon (2023) se muestra que la compensación cinética se cumple para la descomposición térmica de poli (metil metacrilato), de peróxidos orgánicos de masa molecular elevada y carbonato cálcico.
Cuando en un determinado proceso se dan estas compensaciones se puede obtener información sobre el mecanismo de reacción y al mismo tiempo determinar si el proceso está controlado por la entalpía o la entropía. En un trabajo anterior se ha presentado de forma exhaustiva este fenómeno (Garvín et al., 2017), por lo que en este estudio simplemente se exponen de forma simplificada los conceptos utilizados.
Con el fin de describir el mecanismo con el que se lleva a cabo una determinada reacción química se suele utilizar la teoría del estado de transición, en la que los reactantes interaccionan para formar un complejo activado (#) que puede revertir hacia los reactantes o formar el producto o productos finales de la reacción según el siguiente esquema.
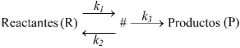
Cuando se desea estudiar un equilibrio termodinámico, la propia constante de equilibrio (Keq) está relacionada con la variación de la energía libre (ΔG), de la entalpía (ΔH) y la entropía (ΔS) según la ecuación de Van’t Hoff (Glasstone, 1949). En el caso de reacciones no reversibles, la relación se aplica a la contante de equilibrio entre los reactantes y el complejo activado:
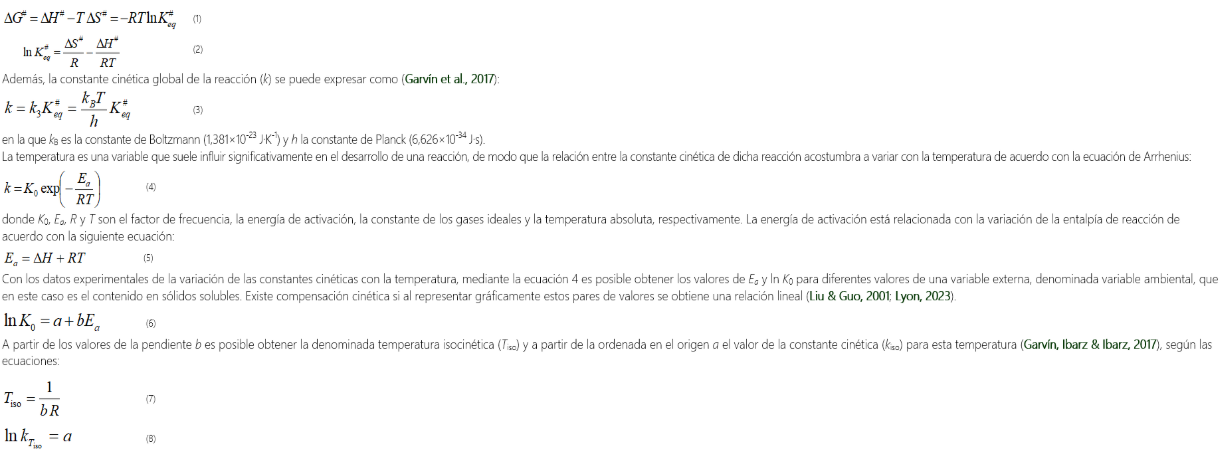
La temperatura isocinética es aquella en que los valores de la constante cinética coinciden cualquiera que sea el valor de la variable ambiental.
Por otra parte, a partir de la ecuación 3 es posible obtener los valores de las constantes de equilibrio del estado de activación (Keq#) a diferentes temperaturas para un determinado valor de la variable medioambiental (sólidos solubles). Con los valores de la constante de equilibrio a diferentes tempera-turas, mediante la ecuación 2, al representar RlnKeq# frente a la inversa de la temperatura absoluta se obtiene una recta cuya pendiente es la variación de entalpía ΔH# y la ordenada en el origen la variación de entropía ΔS# . Existe compensación termodiná-mica, para los diferentes valores de la variable medioambiental, si al representar ΔH# frente a ΔS# existe una relación lineal.
. Existe compensación termodiná-mica, para los diferentes valores de la variable medioambiental, si al representar ΔH# frente a ΔS# existe una relación lineal.
en la que n es el número de temperaturas utilizadas en el estudio de la cinética de reacción y Ti cada una de estas temperaturas.
Al comparar los valores de las temperaturas isocinéticas con la temperatura media armónica es posible determinar si la compensación es real o bien es el resultado de la propagación de errores experimentales. En el caso que el valor de la temperatura media armónica no esté incluido en el intervalo de confianza de la temperatura isocinética, se puede considerar que la compensación estudiada es real (Garvín et al., 2017; Krug et al., 1976). Asimismo, es posible determinar si el control de la reacción es entálpico o entrópico, de modo que, si las temperaturas de trabajo son menores que la temperatura isocinética, el control será entálpico; en caso contrario, el control es entrópico (Garvín et al., 2017).
El objetivo del presente artículo es llevar a cabo un estudio para comprobar si se cumple la compensación cinética y termodinámica en zumos clarificados de limón, utilizando las constantes cinéticas de pardeamiento no enzimático obtenidas en un trabajo anterior (Ibarz et al., 2010), donde la variable ambiental es el contenido en sólidos solubles.
Este estudio permitirá obtener las temperaturas isocinéticas con el fin de determinar si la compen-sación cinética y termodinámica es real. Asimismo, se podrá determinar si el control de la reacción de pardeamiento de estos zumos es entálpico o entrópico.
2. Metodología
De un trabajo anterior (Ibarz et al., 2010) se han tomado los datos de las constantes cinéticas de pardeamiento no enzimático de zumos clarificados de limón con el fin de llevar a cabo un estudio sobre la compensación cinética y termodinámica. En el citado trabajo se estudió la cinética de pardeamiento no enzimático de dichos zumos a diferentes temperaturas de trabajo (70, 80, 90 y 95 ºC) para muestras de zumo con diferente contenido en sólidos solubles (1, 20, 35, 50 y 64,6 ºBrix). Se utilizó la evolución de la absorbancia a 420 nm (A420) y la luminosidad (L*) con el tiempo de tratamiento para obtener las constantes cinéticas del pardeamiento de los zumos. La evolución de estos dos pará-metros colorimétricos se ajustó a cinéticas de orden cero. Para obtener con más detalle la metodología de tratamiento de las muestras y obtención de las constantes cinéticas se puede consultar el citado artículo. Con los valores de las constantes cinéticas se ha llevado a cabo el estudio de compensación cinética y termodinámica utilizando las ecuaciones descritas en la introducción.
En la Figura 1 se muestra el algoritmo utilizado en el estudio de la compensación cinética y termodi-námica. Todas las regresiones utilizadas en el presente artículo se han obtenido a partir del paquete estadístico STATGRAPHICS Centurion XVI (Statistical Graphics Corp., Warrenton, VA, USA), utilizando un nivel de probabilidad del 95%.
3. Resultados y discusión
Del artículo de Ibarz et al. (2010) se han tomado los datos de las constantes cinéticas del pardeamiento de zumos de limón de diferente contenido en sólidos solubles tratados a diferentes temperaturas. En la Tabla 1 se muestran los datos de estas constantes para la evolución de la absorbancia a 420 nm (A420) y la luminosidad (L*), adecuando los valores a las cifras significativas que marca el intervalo de variación de cada parámetro. En el caso de la evolución de A420 con el tiempo su valor aumenta con el tiempo de tratamiento y los datos experimentales se ajustaron a una cinética de orden cero. L* disminuye con el tiempo de tratamiento y también se ajustó a una cinética de orden cero. En la Tabla 1, tanto para A420 como para L*, se puede observar que los valores de las constantes cinéticas aumentan con la temperatura y el contenido en sólidos solubles, es decir, cuanto mayor es la concentración y la temperatura de trabajo más rápidamente se pardearán los zumos. Para un determinado contenido en ºBrix, el valor de la constante cinética aumenta con la temperatura. Para una determinada temperatura el valor de la constante cinética aumenta con el contenido en sólidos solubles.
Tabla 1
Parámetros del modelo cinético de orden cero para la evolución con el tiempo de tratamiento de A420 y L* en zumos clarificados de limón
C | T | kA420×103 | R2 | | kL×102 | R2 |
(ºBrix) | (ºC) | (u.A420·min-1) | | | (u.L*· min-1) | |
64,6 | 70 | 2,2 | 0,9736 | | 6,69 | 0,9880 |
| 80 | 5,5 | 0,9906 | | 13,98 | 0,9870 |
| 90 | 7,3 | 0,9734 | | 20,23 | 0,9914 |
| 95 | 8,9 | 0,9191 | | 27,90 | 0,9541 |
50 | 70 | 1,3 | 0,9861 | | 3,96 | 0,9924 |
| 80 | 3,2 | 0,9950 | | 8,88 | 0,9964 |
| 90 | 6,2 | 0,9738 | | 15,3 | 0,9900 |
| 95 | 7,8 | 0,9758 | | 21,81 | 0,9950 |
35 | 70 | 0,8 | 0,9565 | | 2,32 | 0,9890 |
| 80 | 1,9 | 0,9978 | | 5,29 | 0,9976 |
| 90 | 3,6 | 0,9870 | | 8,97 | 0,9880 |
| 95 | 5,8 | 0,9950 | | 14,20 | 0,9918 |
20 | 70 | 0,5 | 0,9902 | | 1,07 | 0,9577 |
| 80 | 1,2 | 0,9922 | | 3,48 | 0,9704 |
| 90 | 2,3 | 0,9940 | | 5,55 | 0,9882 |
| 95 | 3,3 | 0,9773 | | 8,49 | 0,9779 |
10 | 70 | 0,4 | 0,9579 | | 1,14 | 0,7405 |
| 80 | 0,9 | 0,9920 | | 2,79 | 0,9700 |
| 90 | 1,7 | 0,9837 | | 4,66 | 0,9643 |
| 95 | 2,2 | 0,9851 | | 6,12 | 0,9667 |
Modelos cinéticos: A = A0 + kA420 t; L* = L0* - kL t.
3.1. Compensación cinética
A partir de los datos de la variación de las constantes cinéticas con la temperatura es posible cuantificar el efecto que esta variable ejerce sobre dichas constantes. Para ello, se utiliza la ecuación de Arrhenius (Ec. 4) y con los datos de la Tabla 1 se obtienen los parámetros de esta ecuación para un determinado contenido en sólidos y para cada una de las variables colorimétricas estudiadas. En la Tabla 2 se presentan los resultados de los ajustes, obteniendo que tanto el ajuste como los valores estimados de los parámetros de este ajuste son significativos a un nivel de probabilidad del 95%.
Tabla 2
Parámetros de la ecuación de Arrhenius para la evolución de las diferentes variables colorimétricas
Variable | C | Ea | ln K0 | R2 |
(ºBrix) | (kJ/mol) | (*) |
A420 | 64,6 | 56,54 | 13,830 | 0,9353 |
| 50 | 75,65 | 19,943 | 0,9906 |
| 35 | 80,92 | 21,258 | 0,9958 |
| 20 | 78,25 | 19,874 | 0,9972 |
| 10 | 71,73 | 17,367 | 0,9972 |
L* | 64,6 | 57,60 | 17,549 | 0,9833 |
| 50 | 70,08 | 21,383 | 0,9949 |
| 35 | 73,25 | 21,949 | 0,9916 |
| 20 | 83,20 | 24,757 | 0,9682 |
| 10 | 69,42 | 19,945 | 0,9847 |
(*) K0 en (u.color min-1 ).
Ecuación de Arrhenius: 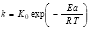
Para determinar si existe compensación cinética, para cada una de las variables colorimétricas (A420 y L*) al representar los valores de lnK0 frente a los de Ea, se debe obtener una relación lineal (Ec. 6) (Garvín et al., 2017). Tomando los datos presentados en la Tabla 2 se puede construir la Figura 2, donde se observa que, tanto para A420 como L*, los pares de valores lnK0 - Ea, para las distintas muestras con diferente contenido en sólidos solubles, siguen una tendencia lineal, lo que corrobora que existe compensación cinética.
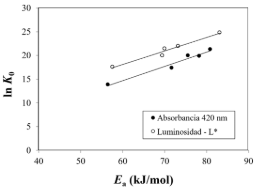
Figura 2. Compensación cinética. Unidades de K0: (u.color min-1).
El ajuste lineal de los datos mostrados en la Figura 2 permite encontrar los parámetros de la ecuación 6. Tanto el ajuste como los valores estimados de los parámetros han resultado significativos a un nivel de probabilidad del 95%. En la Tabla 3 se muestran los valores obtenidos para los parámetros a y b de la ecuación 6. Con el valor de la pendiente (parámetro b), utilizando la ecuación 7 es posible determinar el valor de la temperatura isocinética; mientras que con el valor de la ordenada en el origen (parámetro a), utilizando la ecuación 8 se obtiene el valor de la constante cinética a esta temperatura. En el caso del parámetro A420 se ha obtenido que el valor de la temperatura isocinética es 126,6 ºC y la constante cinética a esta temperatura 0,033 u.A420·min-1. Ambos valores determinan el denominado punto isocinético que representa la temperatura en la que el valor de la constante cinética coincide cualquiera que sea el contenido en sólidos solubles de las muestras. Sin embargo, este es un punto teórico extrapolado del comportamiento estudiado en un rango concreto de temperaturas. En este caso no es real, ya que, a la temperatura de 126,6 ºC las muestras ya no estarían en forma líquida y, por tanto, no es posible confirmarlo de forma experimental. Para el parámetro de luminosidad L*, el valor de la temperatura isocinética que se obtiene es de 149,7 ºC y un valor de la constante cinética de 2,71 u.L*·min-1. Con la luminosidad se presenta la misma situación que el caso de la absorbancia a 420 nm, ya que a esta temperatura isocinética es imposible determinar experimentalmente que el valor de la constante cinética para todas las muestras con distinto contenido en sólidos solubles posee el mismo valor, ya que cualquier disolución alcanzará la ebullición antes de alcanzar dicha temperatura isocinética. Los valores de las temperaturas isocinéticas que se han obtenido en el presente trabajo son similares a las obtenidas en el pardeamiento no enzimático de zumos clarificados de pera (Ibarz et al., 2023).
Tabla 3
Parámetros de compensación cinética para el ajuste a la ec. 6
Parámetro | Unidades | A420 | L* |
a | | 0,30 ± 0,03 | 0,285 ± 0,030 |
b | (mol·kJ-1) | -3,40 ± 2,42 | 0,996 ± 2,110 |
R2 | | 0,9649 | 0,9682 |
Tiso | (ºC) | 126,6 ± 39,6 | 149,7 ± 49,4 |
kTiso | (u.color·min-1) | 0,033 | 2,71 |
Ecuación 6: 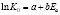
Por otra parte, los valores de las temperaturas experimentales a las que se han desarrollado los tratamientos térmicos de las muestras son inferiores a la temperatura isocinética, tanto para la variable A420 como L*, por lo que las reacciones de pardeamiento térmico de los zumos clarificados de limón estarán controladas por la temperatura. Esto indica que el control de la reacción es entálpico y que la agitación no ejercerá un efecto tan significativo en el desarrollo del proceso global del pardeamiento como lo ejerce el cambio de la temperatura de tratamiento (Garvín et al., 2017).
El control entálpico tendrá lugar a cualquier temperatura de trabajo inferior a la temperatura isocinética. Por lo tanto, por debajo de la temperatura isocinética se verá más afectado por un cambio en la temperatura que por un aumento en la agitación. Dado que interesa evitar el pardeamiento, interesará trabajar a temperaturas lo más bajas posible, sin que exista ningún límite inferior desde el punto de vista de la compensación. La temperatura óptima de trabajo dependerá del tipo de proceso y producto que se desea obtener. Así, en el caso de tratamientos térmicos de pasteurización es esencial controlar que el contenido microbiano del producto final obtenido sea el adecuado. En el contexto de un tratamiento térmico, la temperatura mínima de trabajo será la que suponga la reducción deseada en un tiempo de tratamiento razonable. Además, se deberá fijar el valor que no debe superar el parámetro colorimétrico (A420 y L*); para ello, se aconsejaría trabajar a una temperatura de unos 70 ºC, pero esto alargaría los tiempos de procesado. En el caso que se desee llevar a cabo un proceso de concentración del zumo, utilizando una etapa de evaporación, con el fin de que el producto no se pardee en exceso, es aconsejable que la cámara de evaporación no supere los 60 – 70 ºC, con lo que será necesario fijar una presión inferior a la atmosférica en dicha cámara para que el zumo hierva a esta temperatura.
El valor de la temperatura media armónica de las temperaturas de trabajo se obtiene de la expresión (Ec. 12):
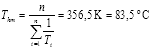
En la Tabla 3 se dan los intervalos de variación de las temperaturas isocinéticas, tanto para A420 como para L*, y en ambos casos se observa que el valor de la temperatura media armónica cae fuera de estos intervalos. Esto indica que se puede admitir que existe una compensación real (Krug et al., 1976; Garvín et al., 2017).
3.3. Compensación termodinámica
Con los valores de las constantes cinéticas que se muestran en la Tabla 1 se pueden calcular los valores de las entalpías y entropías del equilibrio asociado al estado de transición. Tal como se ha indicado en el apartado de Introducción, con la ecuación 3 es posible determinar los valores de la constante de equilibrio del estado de transición (Keq#) y, además, a partir de la ecuación 2 se pueden obtener los valores de la entalpía (ΔH#) y entropía (ΔS#) del estado de transición. En la Tabla 4 se muestran los valores de ΔH# y ΔS# que se han obtenido para las dos variables colorimétricas estudiadas a los diferentes valores de sólidos solubles. Tanto los ajustes como los valores estimados de los parámetros han resultado significativos a un nivel de probabilidad del 95%.
Tabla 4
Valores estimados de la entalpía de activación y entropía de activación para la evolución de las diferentes variables colorimétricas
Variable | C | 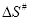
| 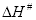
| R2 |
(ºBrix) | (J·mol-1·K-1) | (J·mol-1) |
A420 | 64,6 | -173,70 | 53586,63 | 0,9282 |
| 50 | -122,91 | 72700,32 | 0,9898 |
| 35 | -111,98 | 77965,63 | 0,9954 |
| 20 | -123,49 | 75300,81 | 0,9969 |
| 10 | -144,33 | 68773,96 | 0,9953 |
L* | 64,6 | -142,82 | 54651,76 | 0,9814 |
| 50 | -110,94 | 67130,18 | 0,9944 |
| 35 | -106,24 | 70300,11 | 0,9909 |
| 20 | -82,90 | 80242,93 | 0,9658 |
| 10 | -122,90 | 66472,05 | 0,9833 |
Ecuación (2): 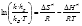
Si existe compensación termodinámica, al representar los valores de ΔH# frente a los valores de ΔS# se debe obtener una relación lineal. En la Figura 3 se muestra la gráfica obtenida, tanto para la variable A420 como L*, donde se observa que existe esta relación lineal, por lo que existe compensación termodinámica para ambas variables.
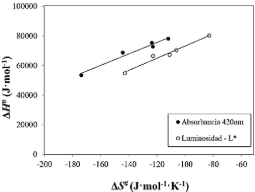
Figura 3. Compensación termodinámica.
Los datos expuestos en la Figura 3 se han ajustado a una línea recta por el método de los mínimos cuadrados obteniendo que tanto los ajustes como los valores estimados de los parámetros han resultado significativos a un nivel de probabilidad del 95%. En la Tabla 5 se muestran los valores de los parámetros A y B del ajuste a la ecuación 9. La pendiente de esta recta (B) se corresponde con la temperatura de isoequilibrio (Tisoeq), mientras que la ordenada en el origen es el valor de la variación de la energía libre de Gibbs (ΔG#isoeq) para esta temperatura de isoequilibrio. A partir de este último valor es posible determinar la constante de equilibrio para el estado de transición (K#isoeq) a esta temperatura.
Para la variable A420 se observa que el valor de la temperatura de isoequilibrio es de 112,8 ºC, siendo 121862 J/mol el valor de la energía libre de Gibbs para el estado de transición a esta temperatura, mientras que la constante de equilibrio del estado de transición presenta un valor de 3,17×10-17. En el caso de la variable L*, en la Tabla 5 se puede observar que la temperatura de isoequilibrio posee un valor de 136,3 ºC, con una energía libre de Gibbs a esta temperatura de 114071 J/mol y una constante de equilibrio del estado de transición de 2,76×10-15. Las temperaturas de isoequilibrio obtenidas son similares a las obtenidas en el pardeamiento no enzimático de zumos clarificados de pera (Ibarz et al., 2023). En cada una de las variables colorimétricas estudiadas, para la temperatura de isoequilibrio, los valores de las constantes de equilibrio del estado de transición deben ser iguales para todas las muestras cualquiera que sea el contenido en sólidos solubles. Sin embargo, como las temperaturas de isoequilibrio presentan unos valores elevados es imposible determinar experimentalmente esta coincidencia en los valores de las constantes de isoequilibrio.
Tabla 5
Parámetros de compensación termodinámica para el ajuste a la ecuación 9
Pará-metro | Unidades | A420 | L* |
A | (J·mol-1) | 121862 ± 5831 | 114071 ± 4914 |
B | (K) | 385,8 ± 42,6 | 409,3 ± 42,8 |
R2 | | 0,9649 | 0,9683 |
Tisoeq | (ºC) | 112,8 ± 42,6 | 136,3 ± 42,8 |
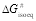
| (J·mol-1) | 121862 | 114071 |
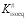
| | 3,17×10-17 | 2,76×10-15 |
Ecuación 9: 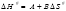
Para ambas variables (A420 y L*) se han obtenido temperaturas de isoequilibrio superiores a las temperaturas de trabajo, por lo que, del mismo modo que ocurría con la compensación cinética, el proceso global del pardeamiento no enzimático de los zumos clarificados de limón está controlado por la entalpía. Así, entre las variables externas que pueden influir sobre este tipo de proceso (temperatura y/o agitación), la temperatura es la que ejerce un efecto más pronunciado (Garvín et al., 2017).
Por otra parte, en el caso de la variable colorimétrica A420, se observa que la temperatura media armónica de las todas las temperaturas de trabajo (Thm = 83,5 ºC) está incluida dentro del intervalo de variación de la temperatura de isoequilibrio, ya que ésta varía entre 70,2 ºC y 155,4 ºC, lo que indica que no se puede afirmar que esta compensación termodinámica sea real, sino que podría ser debida a la acumulación de errores experimentales (Krug et al., 1976; Garvín et al., 2017). Sin embargo, para la variable colorimétrica L*, el valor de la temperatura media armónica no cae dentro del intervalo de variación de la temperatura de isoequilibrio, cuyos límites inferior y superior son 93,5 ºC y 179,01 ºC, de modo que en este caso sí que se puede afirmar que la compensación termodinámica es real.
4. Conclusiones
El pardeamiento no enzimático de zumos clarificados de limón debido a los tratamientos térmicos se describe siguiendo la evolución de parámetros colorimétricos (A420 y L*) que se ajusta a una cinética de orden cero. Se trata de una reacción irreversible en cuyo mecanismo se supone la formación de un complejo activado o estado de transición (#), que puede revertir hacia los reactantes o formar los productos finales de la reacción.
Se ha observado que el proceso global de estas reacciones de pardeamiento cumple las relaciones lineales de las compensaciones cinética y termodinámica. Para el parámetro colorimétrico A420 se han obtenido un valor de la temperatura isocinética de 126,6 ºC y una temperatura de isoequilibrio de 112,8 ºC. Para el parámetro L*, la temperatura isocinética ha sido de 149,7 ºC y la de isoequilibrio de 136,3 ºC. Se ha observado que existe compensación cinética y termodinámica para el pardeamiento de zumos clarificados de limón, por lo que el mecanismo de esta reacción se mantiene para todas las temperaturas de trabajo y para el rango estudiado de contenidos en sólidos solubles. Además, como las temperaturas isocinética y de isoequilibrio son superiores a las temperaturas de trabajo, la cinética de reacción estará controlada entálpicamente. Por lo tanto, para evitar el deterioro de estos zumos se aconseja intervenir en la temperatura de trabajo, intentando que el tratamiento térmico se lleve a cabo a la menor temperatura posible.
Contribución de autores
Conceptualización: R.I., A.G., O.T. y A.I.; Gestión de datos: R.I., A.G., O.T. y A.I.; Análisis formal: R.I., A.G., O.T. y A.I.; Adquisición de financiación: A.I.; Investigación: R.I., y O.T.; Metodología: R.I., y O.T.; Administración de proyecto: A.G. y A.I.; Recursos: A.G. y A.I.; Software: R.I. y A.G.; Supervisión: A.G. y A.I.; Validación: R.I., y O.T.; Visualización: R.I., A.G., O.T. y A.I.; Escritura – manuscrito original: R.I., A.G., O.T. y A.I.; Escritura– revisión y edición: R.I., A.G. y A.I.
Declaración de Conflicto de Intereses
No existe ningún conflicto de interés de los autores.
ORCID
R. Ibarz https://orcid.org/0000-0002-5559-0912
A. Garvín https://orcid.org/0000-0003-2569-3432
O. Tomasa https://orcid.org/0000-0003-4077-4177
A. Ibarz https://orcid.org/0000-0003-0673-5174
Referencias bibliográficas
Aguilar, K., Garvín, A., Azuara, E., & Ibarz, A. (2016). Rate-Controlling Mechanisms in the Photo-degradation of 5-Hydroxymethylfurfural. Food Bioprocess Technology, 9, 1399-1407. https://doi.org/10.1007/s11947-016-1729-7
Beveridge, T., & Harrison, J.E. (1984). Nonenzymatic browning in pear juice concentrate at elevated temperatures, Journal Food Science, 49, 1335-1340. https://doi.org/10.1111/j.1365-2621.1984.tb14984.x
Beristain, C. I., Garcia, H. S., & Azuara, E. (1996). Enthalpy-entropy compensation in food vapor adsorption. Journal of Food Engineering, 30, 405–415. https://doi.org/10.1016/S0260-8774(96)00011-8
Cornwell, C.J., & Wrolstad, R.E. (1981). Causes of browning in pear juice concentrate at elevated temperatures. Journal Food Science, 46, 515-518. https://doi.org/10.1111/j.1365-2621.1981.tb04899.x
Echavarría, P., Pagán, J. & Ibarz, A. (2016). Kinetics of color development in glucose/Amino Acid model systems at different temperatures. Scientia Agropecuaria, 7(1), 15-21. https://doi.org/10.17268/sci.agropecu.2016.01.02
Garvín, A., Ibarz, R., & Ibarz, A. (2017). Kinetic and thermodynamic compensation. A current and practical review for foods. Food Research International, 96, 132-153. https://doi.org/dx.doi.org/10.1016/j.foodres.2017.03.004
Garvín, A., Augusto, P. E. D, & Ibarz, A. (2019). Kinetic and thermodynamic compensation study of the hydration of faba beans (Vicia faba L.). Food Research International, 119, 390-397. https://doi.org/10.1016/j.foodres.2019.02.002
Glasstone, S. (1949). Textbook of physical chemistry. New York: Ed. D Van Nostrand Company Inc.
Hotta, M. & Koga, N. (2024). Extended kinetic approach to reversible thermal decomposition of solids: A universal description considering the effect of the gaseous product and the kinetic compensation effect. Thermochimica Acta, 733, 179699. https://doi.org/10.1016/j.tca.2024.179699
Ibarz, R., Pagán, J., Garza, S., & Ibarz, A. (2010). Pardeamiento de zumos clarificados de limón tratados a altas temperaturas. Scientia Agropecuaria, 1, 7-20. https://doi.org/10.17268/sci.agropecu.2010.01.01
Ibarz, R., Garvín, A., & Ibarz, A. (2017). Kinetic and thermodynamic study of the photochemical degradation of patulin. Food Reserach International, 99, 348-354. https://doi.org/10.1016/j.foodres.2017.05.025
Ibarz, R., Garvín, A., & Ibarz, A. (2023). Estudio cinético y termodinámico del pardeamiento no enzimático de zumos clarificados de limón. AgroScience Research, 1(1), 3-11. https://doi.org/10.17268/agrosci.2023.001
Jankovic, B., Manic, N., Popovic, M., Cvetkovic, S., Dzeletovic, Z. & Stojiljkovic, D. (2023). Kinetic and thermodynamic compensation phenomena in C3 and C4 energy crops pyrolysis: Implications on reaction mechanisms and product distributions. Industrial Crops & Products, 194, 116275. https://doi.org/ 10.1016/j.indcrop.2023.116275
Krug, R.R., Hunter, W.G., & Grieger, R.A. (1976). Enthalpy-entropy compensation. 1. Some fundamental statistical problems associated with the analysis of Van’t Hoff and Arrhenius data. The Journal of Physical Chemistry, 80(21), 2335-2341. https://doi.org/10.1021/j100562a006
Liu, L., & Guo, Q. (2001). Isokinetic relationship, isoequilibrium relationship, and enthalpy-entropy compensation. Chemical Reviews, 201, 673–695. https://doi.org/10.1021/cr990416z
Lyon, R.E. (2023). A physical basis for kinetic compensation. J. Phys. Chem. A, 127, 2399−2406. https://doi.org/10.1021/acs.jpca.2c07715
Manayay, D., & Ibarz, A. (2010). Modelamiento de la cinética de reacciones del pardeamiento no enzimático y el comportamiento reológico, en el proceso térmico de jugos y pulpas de fruta. Scientia Agropecuaria, 1, 155-168. https://doi.org/10.17268/sci.agropecu.2010.02.06
Özilgen, M., & Bayindirli, L. (1992). Frequency factor-activation energy compensation relations for viscosity of the fruit juices. Journal of Food Engineering, 17, 143-151. https://doi.org/10.1016/0260-8774(92)90057-D
Salinas, D., Garvín, A., Ibarz, R., & Ibarz, A. (2019). Effect of apple fibre addition and temperature on the rheological properties of apple juice and compensation study. LWT-Food Science and Technology, 116, 108456. https://doi.org/10.1016/j.lwt.2019.108456
Salinas, D., Garvín, A., Ibarz, R., & Ibarz, A. (2021). Viscoelastic properties and compensation study of apple juice enriched with apple fiber. LWT-Food Science and Technology, 151, 111971. https://doi.org/10.1016/j.lwt.2021.111971
Toribio, J.L., Lozano, J.E. (1986). Heat induced Browning of clarified Apple juice at high temperatures. Journal Food Science, 51(1), 172-175. https://doi.org/10.1111/j.1365-2621.1986.tb10863.x
Waller, G.R., & Feather, M.S. (1983). Maillard Reaction in Foods and Nutrition. ACS Symposium series 215. Am. Chem. Soc. Washington
Wang, X., Wang, Y., Guo, J., Zhao, Y., Wang, X., Zhang, X., & Chen, Z. (2024). Behaviors and non‑isothermal kinetics of Chlorella pyrenoidosa fodder pyrolysis by a modified kinetic compensation effects and a parallel two‑step reaction model. Biomass Conversion and Biorefinery, 14, 5589–5600. https://doi.org/10.1007/s13399-022-02723-7
. Existe compensación termodiná-mica, para los diferentes valores de la variable medioambiental, si al representar ΔH# frente a ΔS# existe una relación lineal.