1. Introducción
Las industrias agropecuarias y acuícola dependen de fuentes de materia prima de origen vegetal y animal, que genera demanda de harina y aceite de pescado, elementos esenciales en la fabricación del alimento balanceado comercial obtenido a partir de las capturas de peces pelágicos pequeños, entre ellos, la anchoveta (Engraulis ringens).
La anchoveta es una de las especies marinas más importantes a nivel mundial debido a su rol en la producción de harina y aceite; siendo Perú el mayor productor de harina de pescado, debido a los grandes “stocks” de la especie, existentes frente a sus costas. La distribución y abundancia de la especie depende de las fluctuaciones de la temperatura del mar, influenciada por fenómenos climáticos como El Niño y La Niña, que condicionan las capturas pesqueras, generando cambios en la oferta y demanda de la harina de pescado y repercutiendo en los precios en el mercado global.
La temperatura superficial del mar (TSM) constitu-ye una característica reconocida de la oceanogra-fía de un área, presentando variabilidad en espacio y tiempo. Entre los efectos sobre las pesquerías se destacan: la migración vertical u horizontal, la distribución geográfica de los stocks y la alteración de sus ciclos de vida (Cheung et al., 2009 y García et al., 2013); así como, las actividades reproductivas, la disponibilidad de alimento (Richardson & Schoeman, 2004) y la productividad marina (Lehodey et al., 2006; Hsieh et al., 2019). En el mismo contexto, los efectos del incremento de la temperatura marina vinculados al Cambio Climático, parecen estar afectando los ecosistemas, formulando desafíos trascenden-tales en términos de sostenibilidad.
En la costa sur de Ecuador, Perú y norte de Chile se presentan afloramientos marinos, que provo-can el ascenso de aguas profundas frías y nutrientes hacia la superficie cambiando la dinámica de la temperatura del Pacífico suroriental (Montecinos & Aceituno, 2003; Arntz et al., 2006). Esta productividad biológica sustenta la pesquería de pelágicos pequeños, más impor-tantes del mundo, contribuyendo a la biodiver-sidad marina en la región (Chavez & Messié, 2009). La ocurrencia de El Niño debilita los aflora-mientos favoreciendo las condiciones cálidas.
Las condiciones cálidas de los eventos El Niño pueden provocar cambios en la estructura trófica en los ecosistemas de pelágicos pequeños alterando la extracción, con implicaciones sobre la seguridad alimentaria, la economía y la gestión pesquera de los países afectados (García-Reyes et al., 2014; Fisher et al., 2015). Las anomalías cálidas a nivel superficial y subsuperficial, provo-can migraciones generalmente temporales de especies hacia zonas más favorables, afectando su disponibilidad pesquera (Cai et al., 2014; Chavez et al., 2017).
Por otra parte, la producción de harina de pescado es una actividad económica que se basa en la captura y procesamiento de pelágicos pequeños, obtenida mediante la cocción, secado y molienda del recurso. En la industria agropecuaria y acuícola es utilizada como fuente de proteínas y nutrientes para la producción de alimento (Gutiérrez et al., 2007; Tafur et al., 2009; Pauly & Zeller, 2017).
Según el Anuario Estadístico de la Organización Internacional de la Harina y Aceite de Pescado - IFFO (Rodríguez, 2023), Perú es el primer productor mundial de harina de pescado con 1,1 millones de TM, Chile con 369 mil TM ocupa el cuarto lugar; mientras que, Ecuador con 85 mil TM se encuentra en la décimo quinta posición. Por su parte, E. ringens es la única especie permitida por el estado peruano para esta industria, que constituye el principal indicador de la producción de harina de pescado en el área (IMARPE, 2020), y la que impone el precio mundial.
En este marco, la pesquería de E. ringens es considerada una de las más grandes y sostenibles del mundo, constituyendo una transcendental fuente de ingresos económicos (Chavez et al., 2003) y la gestión adecuada es decisiva para garantizar la continuidad de la actividad (Fréon et al., 2005; Ñiquen y Bouchon 2004), así como la conservación de los ecosistemas marinos (Christy, 2011; Carlson, 2018). E. ringens ha experimentado fluctuaciones significativas en su abundancia debido a factores ambientales y a la presión pesquera.
Por su parte, Bracamonte (2025) y Burga Farfán et al. (2024) han estudiado la cadena de valor de la harina de pescado y la fluctuación en su precio a nivel local e internacional, determinando los elementos con capacidad de afectar esta industria en el Perú. El precio de la harina es cambiante y su producción está sujeta a regulaciones ambientales y de calidad para garantizar la seguridad alimentaria y la sostenibilidad de la actividad (FAO, 2009; FAO, 2014).
De este modo, las series de tiempo captan las tendencias y estacionalidades que afectan estos fenómenos, identificando patrones recurrentes y posibles factores externos que inciden en su comportamiento. Por tanto, la TSM juega un rol preponderante en la dinámica de los ecosistemas marinos y, por ende, en la disponibilidad de la anchoveta.
Una de las metodologías usualmente empleadas en el Análisis de Series de Tiempo (AST) es el modelo ARIMA (AutoRegresive Integrated Moving Average), y se aplica en caso de que la serie de tiempo sea no estacionaria (De la Fuente, 2013); mientras que, para series estacionarias (media, varianza y autocorrelación no varían con el tiempo) se utiliza el modelo ARMA (Auto-regressive Moving Average), en el que intervienen componentes autorregresivos (AR) y de media móvil (MA). La ecuación general del modelo ARMA (p, q) se expresa de la siguiente forma:
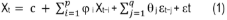
Donde Xt: variable de la serie observada en el tiempo t (como la TSM o el precio de la harina de pescado); c: intercepto o constante que repre-senta la tendencia central de la serie; p: orden del componente autoregresivo (AR), es decir, valores pasados de la serie que afectan al valor presente; i: coeficiente del componente autorregresivo, determinan la influencia de los valores pasados, Xt−i; q: orden del componente de media móvil (MA), que indica cuántos errores pasados afectan al valor presente; Xt−i: valores pasados de la serie, que influyen en el valor actual Xt; j: coeficientes del componente de media móvil, miden la influencia de los errores pasados t−j sobre Xt; t: error aleatorio en el tiempo (t) y t−j: errores pasados, que afectan al valor presente a través del componente de media móvil.
Para estudiar la relación entre la TSM y los desembarques de anchoveta, el modelo ARIMA es útil para descomponer la variabilidad inherente a las series de tiempo en componentes predecibles y aleatorios; esto permite identificar patrones estacionales o ciclos recurrentes en la temperatura. Previo a la aplicación del modelo, es preponderante corroborar que los datos cumplan los supuestos de estacionariedad, y en un escenario opuesto, se aplican técnicas de diferenciación de la serie. Scheidereite & Faure (2015) y Cancino et al., (2023) sostienen que el uso de ARIMA en estudios de la relación de parámetros climáticos y económicos ha demostrado eficacia en la estimación de correlaciones y predicciones a corto plazo.
Al revisar la literatura científica, existe escasa evidencia de la predicción de modelos que permitan anticipar cambios en la producción y precio. De modo que, el entendimiento de los factores que influyen en las capturas de anchoveta y la relación con el precio de la harina de pescado es esencial para la administración, planificación y la sostenibilidad de los recursos hidrobiológicos.
Las variaciones en la temperatura superficial del mar, son cada vez más frecuentes debido al cambio climático, teniendo impacto directo sobre los ecosistemas marinos y en poblaciones de peces. Al estudiar esta relación, la investigación no solo contribuirá al conocimiento científico sobre el comportamiento de las especies, sino que ofrecerá información para predecir los efectos adversos en las pesquerías y ser utilizados por organismos de gestión pesquera para la toma de decisiones, permitiendo desarrollar estrategias efectivas para mantener la sostenibilidad de los recursos pesqueros y garantizar la estabilidad del mercado. Por ello, el análisis de series de tiempo de las variables permitirá generar modelos predictivos que ayuden a anticipar la influencia de las fluctuaciones climáticas sobre los recursos pesqueros y los mercados asociados.
La investigación consistió en analizar la relación entre la TSM y los desembarques de E. ringens mediante modelos ARIMA para la proyección del precio de la harina de pescado.
2. Metodología
El trabajo se enfocó en el análisis de las capturas pesqueras anuales de E. ringens desembarcadas en las zonas norte y centro de Perú, repre-sentadas climáticamente por el área Niño 1+2 (Figura 2).
El tipo de investigación fue cuantitativo, longitu-dinal y correlacional. El enfoque cuantitativo se basó en la recopilación y análisis de series de tiempo anuales de TSM promedio (°C), volúme-nes de captura (TM) y precio promedio interna-cional de la harina de pescado (USD), buscando patrones, tendencias o correlaciones estadísticas entre las variables; mientras que fue longitudinal debido a que se estudiaron los cambios de estas variables a través del tiempo; y, por último, fue correlacional al buscar establecer relaciones entre las variables.
La TSM del área Niño 1+2 (°C), definida por el Centro de Predicción Climática de la Adminis-tración del Océano y la Atmósfera de los Estados Unidos de América – CPC NOAA (Climate Prediction Center - Four El Niño Regions, 2023), es expresada en un área entre 0 a 10° sur y entre 80 a 90° oeste. Esta región cubre el área marina frente a la costa sur de Ecuador y norte de Perú.
Tabla 4
Correlogramas de la AC y ACP de la serie de precio de la harina de pescado
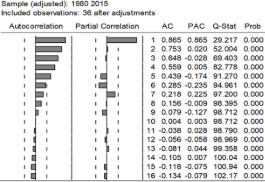
Los resultados confirman que los modelos ARIMA aplicados, funcionan mejor en el corto plazo, como ha sido expresado por varios autores. No obstante, la periodicidad anual de las series utilizadas indica que, si las proyecciones son válidas en un ciclo de 1 a 3 años, su aplicabilidad tendría un alcance muy importante. En este contexto, se relacionó la TSM con la serie del precio de la harina de pescado sin tendencia. Luego, las series fueron tratadas con medias móviles de tres períodos con el objeto de filtrar influencias de alta frecuencia. Finalmente, se realizó un proceso de regresión lineal (Figura 8).
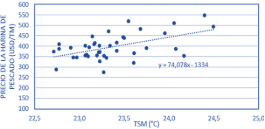
Figura 8. Regresión de la TSM y el precio de la harina de pescado.
La regresión entre la TSM y el precio de la harina de pescado registró un coeficiente r= 0,533, con significancia estadística al 95% de confianza (p = 0,0004). Finalmente, la ecuación se ajustó al promedio de la franja de nueva estabilización de precios que se observó desde aproximadamente el año 2010, obteniéndose la ecuación 2:
Precio harina de pescado = 74,0780 TSM - 247 (2)
Ashok & Yamagata (2009) indican que los patrones de calentamiento y enfriamiento de la superficie del mar en el Pacífico tropical parecen estar cambiando, asociados al calentamiento global, lo que implicaría cambios en el comportamiento de El Niño. En el trabajo de L’Heureux et al. (2013) se reportó tendencias lineales de largo plazo de la TSM mensual en el Océano Pacífico tropical durante el período 1950-2010. En la serie TSM Niño 1+2 analizada se encontró una marcada tendencia positiva, la cual fue filtrada, generando una serie centrada en la variabilidad climática de corto período interanual. La serie de TSM obtenida permitió diferenciar los eventos climáticos en sus distintas intensidades.
La serie de capturas evidencia el efecto El Niño sobre la pesquería y determina el potencial efecto de la administración pesquera posterior al colapso de los stocks de E. ringens. Las medidas administrativas produjeron recuperación lenta del stock, afectado por recurrentes El Niño. En estos eventos, disminuye la intensidad de los afloramientos de aguas frías ricas en nutrientes, provocando reducción en la disponibilidad de alimento para los pelágicos pequeños, los cuales migran hacia aguas más frías y profundas en busca de condiciones favorables siendo menos vulnerables a la pesca cerco (Gutiérrez et al., 2007; Espino, 2013).
Chavez et al. (2003) y Ñiquen & Bouchon, (2004) indican que la disminución de E. ringens puede generar un efecto multiplicador en la cadena alimenticia de las especies marinas depreda-doras, y en comunidades costeras que dependen de esta actividad para el sustento. Por ello, para mitigar los impactos de los eventos climáticos en la pesquería, se debe contar con sistemas de monitoreo, control, y pronóstico que permitan responder a las variaciones de las condiciones oceanográficas, promoviendo la sostenibilidad de los recursos pesqueros y la conservación de los recursos marinos (Chavez & Messié, 2009), lo que confirma una correlación significativa entre la TSM y la pesquería.
Timmermann et al. (1999) sostiene que durante época de eventos El Niño, la escasez de E. ringens puede generar el aumento de los costos de producción de la harina de pescado, y por consiguiente un costo elevado en el precio el precio en el mercado. Por otro lado, en eventos de La Niña, evento frío, los crecientes desembarques de anchoveta permiten la existencia de mayor disponibilidad de materia prima, pero un descenso en el precio de la harina. Para esto, se generan estrategias de mercado, como el almacenamiento de harina y aceite de pescado para satisfacer la demanda en períodos de escasez, evitando la venta en períodos de sobreoferta.
Otros factores como la demanda global de productos pesqueros y la competencia en el mercado internacional también influyen en la variabilidad del precio de la harina de pescado (Burga Farfán et al., 2024), lo que resulta parcialmente evidente en la serie de precios. Al filtrar la tendencia del incremento sostenido de los precios en el período 2002–2010, se registró la correlación con significancia estadística, que confirmó el planteamiento de utilizar la TSM como una herramienta para realizar estimaciones del precio de la harina de pescado.
4. Conclusiones
La proyección mediante ARIMA, en aplicación del modelo Box-Jenkins, resultó ser una herramienta eficaz para el AST, y el pronóstico para períodos cercanos (hasta 3 años). En un siguiente paso, en el contexto de la investigación pesquera, sería eficiente trabajar con períodos de meses, en lugar de años, siendo necesario incorporar compo-nentes estacionales en el proceso de determi-nación de los parámetros del ARMA. La relación entre la TSM y las capturas de E. ringens de las zonas Norte+Centro presentó significancia esta-dística al 95% de confianza, aunque con un coeficiente correlación medio. Las series de tiempo reflejan los eventos climáticos más impor-tantes, sin embargo, responden también a otros fenómenos como el cambio climático, aspectos biológicos, y de administración pesquera.
Se estableció tres fases en la variación del precio de la harina de pescado, con un crecimiento lento entre 1980 y 1999, un crecimiento acelerado entre el año 2000 al 2010, distorsión atribuible a variaciones de mercado por una fase de disminución en la oferta de harina, que marcó una nueva estabilización de los precios a partir de esa fecha.
De mantenerse la estabilización de los precios, la proyección ARIMA de la TSM se podría convertir en una herramienta práctica para proyectar el precio de la harina de pescado, la planificación industrial y la estabilidad del mercado interna-cional de harina de pescado, contribuyendo a la sostenibilidad de la pesquería y de las industrias agropecuaria y acuícola.
Referencias bibliográficas
Arntz, W. E., Gallardo, V. A., Gutiérrez, D., Isla, E., Levin, L. A., Mendo, J., & Wolff, M. (2006). El Niño and similar perturbation effects on the benthos of the Humboldt, California, and Benguela Current upwelling ecosystems. Advances in Geosciences, 6, 243-265. https://doi.org/10.5194/adgeo-6-243-2006
Ashok, K., & Yamagata, T. (2009). The El Niño with a difference. Nature, 461(7263), 481-484. https://doi.org/10.1038/461481a
Banco Central de la Reserva de Perú - BCRP, G. C. de E. E. (2022). Pesqueros—Harina de Pescado—Precio (US$ por toneladas).
Bouchon Corrales, M., Ñiquen Carranza, M., & Ttito, H. (2018). Estadísticas de la pesquería pelágica en la costa peruana (1959- 2015). Instituto del Mar del Perú - IMARPE. https://hdl.handle.net/20.500.12958/3302
Box, G. E., Jenkins, G. M., Reinsel, G. C., & Ljung, G. M. (1994). Time series analysis: Forecasting and control (3rd edition). John Wiley & Sons. ISBN-13 978-0130607744. https://doi.org/10.1002/9781118619193
Bracamonte Bazán, G. H. (2025). Tres propuestas de mejora para el proceso productivo de una empresa de harina de pescado. http://hdl.handle.net/20.500.12404/29932
Burga Farfán, J. E., Aguirre Panta, Y. E., Lecarnaqué Arévalo, C. A., & Aldana Yarlequé, C. N. (2024). Predicción de precios de exportación del aceite y la harina de pescado, utilizando series de tiempo para el periodo 2023. Revista de Investigación Científica de la UNF – Aypate, 2(1), 43–53. https://doi.org/10.57063/ricay.v2i1.28
Cai, W., Borlace, S., Lengaigne, M., Van Rensch, P., Collins, M., Vecchi, G., & Cowan, T. (2014). Increasing frequency of extreme El Niño events due to greenhouse warming. Nature Climate Change, 4(2), 111-116. https://doi.org/10.1038/nclimate2100
Cancino, S. E., Escalante, G. O. C., & Ricketts, D. F. C. (2023). Un modelo Box Jenkins ARIMA para modelar y pronosticar la producción de mora de castilla en Colombia. Económicas CUC, 44(1), Article 1. https://doi.org/10.17981/econcuc.44.1.2023.Econ.4
Carlson, A. K., Taylor, W. W., Liu, J., & Orlic, I. (2018). Peruvian anchoveta as a telecoupled fisheries system. Ecology and Society, 23(1). https://doi.org/10.5751/ES-09923-230135
Chavez, F. P., & Messié, M. (2009). A comparison of eastern boundary upwelling ecosystems. Progress in Oceanography, 83(1-4), 80-96. https://doi.org/10.1016/j.pocean.2009.07.032
Chavez, F. P., Messié, M., & Pennington, J. T. (2017). Marine primary production in relation to climate variability and change. Annual Review of Marine Science, 9, 227-260. https://doi.org/10.1146/annurev.marine.010908.163917
Chavez, F. P., Ryan, J., Lluch-Cota, S. E., & Ñiquen, M. (2003). From anchovies to sardines and back: multidecadal change in the Pacific Ocean. Science, 299(5604), 217-221. https://doi.org/10.1126/science.1075880
Cheung, W. W., Lam, V. W., Sarmiento, J. L., Kearney, K., Watson, R., & Pauly, D. (2009). Projecting global marine biodiversity impacts under climate change scenarios. Fish and Fisheries, 10(3), 235-251. https://doi.org/10.1111/j.1467-2979.2008.00315.x
Christy, F. T. (2011). The Development and Management of Marine Fisheries in Latin America and the Caribbean. https://doi.org/10.18235/0008823
Climate Prediction Center - CPC (2023). Four El Niño Regions – NOAA. https://www.cpc.ncep.noaa.gov/products/analysis_monitoring/enso_advisory/ensodisc.shtml
De La Fuente, F. S. (2013). Series Temporales, Modelo ARIMA - Metodología de Box—Jenkins (p. 57). Universidad Autónoma de Madrid. Facultad Ciencias Económicas y Empresariales Departamento de Economía Aplicada.
Espino, M. (2013). El jurel Trachurus murphyi y las variables ambientales de macroescala. Revista Peruana de Biología, 20(1), 09-20.
Fisher, J. L., Peterson, W. T., & Rykaczewski, R. R. (2015). The impact of El Niño events on the pelagic food chain in the northern California Current. Global Change Biology, 21(12), 4401-4414. https://doi.org/10.1111/gcb.13054
Food and Agriculture Organization of the United Nations - FAO. (2009). Guide for the production of fish meal in developing countries. Food and Agriculture Organization of the United Nations. Roma, Italia.
Food and Agriculture Organization of the United Nations- FAO. (2014). The state of world fisheries and aquaculture 2014: Opportunities and challenges. Food and Agriculture Organization of the United Nations. Roma, Italia.
Fréon, P., Cury, P., Shannon, L., Roy, C., & Shin, Y. J. (2005). Sustainable exploitation of small pelagic fish stocks challenged by environmental and ecosystem changes: a review. Bulletin of Marine Science, 76(2), 385-462.
García, H. E., Locarnini, R. A., Boyer, T. P., Antonov, J.I., Mishonov, A.V., Baranova, O.K., Zweng, M.M., Reagan,J.R., Johnson, D.R. (2013). World Ocean Atlas 2013. Vol. 3: Dissolved Oxygen, Apparent Oxygen Utilization, and Oxygen Saturation. S. Levitus, Ed.; A. Mishonov, Technical Ed. NOAA Atlas NESDIS 75, 27 pp.
García-Reyes, M., Largier, J., Sydeman, W. (2014). Synoptic-scale upwelling indices and predictions of phyto-and zooplankton populations. Progress in Oceanography, 120, 177-188. https://doi.org/10.1016/j.pocean.2013.08.004
Gutiérrez, M., Swartzman, G., Bertrand, A., Bertrand, S. (2007). Anchovy (Engraulis ringens) and sardine (Sardinops sagax) spatial dynamics and aggregation patterns in the Humboldt Current ecosystem, Peru, from 1983–2003. Fisheries Oceanography, 16(2), 155-168. https://doi.org/10.1111/j.1365-2419.2006.00422.x
Instituto del Mar del Perú - IMARPE, (2020). Informe sobre las condiciones oceanográficas y la pesquería de anchoveta en la costa peruana. Lima: IMARPE.
Hsieh, C. H., Reiss, C. S., Hunter, J. R., Beddington, J. R., May, R. M., & Sugihara, G. (2019). Fishing elevates variability in the abundance of exploited species. Nature, 443(7113), 859-862. https://doi.org/10.1038/nature05232
L’Heureux, M. L., Collins, D. C., & Hu, Z.-Z. (2013). Linear trends in sea surface temperature of the tropical Pacific Ocean and implications for the El Niño-Southern Oscillation. Climate Dynamics, 40(5), 1223-1236. https://doi.org/10.1007/s00382-012-1331-2
Lehodey, P., Bertignac, M., Hampton, J., Lewis, A., & Picaut, J. (2006). El Niño Southern Oscillation and tuna in the western Pacific. Nature, 389, 715–718 (1997). https://doi.org/10.1038/39575
Montecinos, A., & Aceituno, P. (2003). Seasonality of the ENSO-related rainfall variability in central Chile and associated circulation anomalies. Journal of Climate, 16(2), 281-296. https://doi.org/10.1175/1520-0442(2003)016<0281:SOTERR>2.0.CO;2
Ñiquen, M., & Bouchon, M. (2004) Impact of El Niño events on pelagic fisheries in Peruvian waters, Deep Sea Research Part II: Topical Studies in Oceanography, Volume 5 (6-9) 563-574. https://doi.org/10.1016/j.dsr2.2004.03.001.
Pauly, D., & Zeller, D. (2017). Comments on FAOs State of World Fisheries and Aquaculture (SOFIA 2016). Marine Policy, 77, 176-181. https://doi.org/10.1016/j.marpol.2017.01.006
Richardson, A. J., & Schoeman, D. S. (2004). Climate impact on plankton ecosystems in the Northeast Atlantic. Science, 305(5690), 1609-1612. https://doi.org/10.1126/science.1100958
Rodríguez, J. (2023). Calendario anual de trabajo de la industria de harina pescado en Perú. Veterinaria Digital - Avicultura, Porcicultura, Rumiantes y Acuicultura.
Scheidereite, G. D., & Faure, O. R. (2015). Aplicación de los Modelos Autorregresivos Integrados de Media Móvil (ARIMA) a las Series de Precipitaciones de Lluvia. Revista RInCE, 6(12), 16. https://doi.org/10.54789/rince.12.1
Tafur, R., Paredes, C., Moreno, J., & Ortiz, M. (2009). Overview of the Peruvian anchoveta fisheries. In Anchovy & Its Environment in the Northern Humboldt Current System (pp. 1-13). Springer, Berlin, Heidelberg.
Timmermann, A., Oberhuber, J., Bacher, A., Esch, M., Latif, M., & Roeckner, E. (1999). Increased El Niño frequency in a climate model forced by future greenhouse warming. Nature, 398(6729), 694-697. https://doi.org/10.1038/19505