Uso de la metodología de superficie de respuesta para la optimización del secado de láminas de jengibre (Zingiber Officinale) en microondas y determinación de las condiciones de humedad de equilibrio

Use of the response surface methodology for the optimization of the drying of ginger slices (Zingiber Officinale) in microwaves and determination of the equilibrium moisture conditions

David Vivanco-Pezantes1, *; Domingo Javier Nieto-Freire1

1 Facultad de Ingeniería Pesquera y de Alimentos, Universidad Nacional del Callao. Perú.

ORCID de los autores

D. Vivanco-Pezantes: https://orcid.org/0000-0002-9474-0290

D. J. Nieto-Freire: https://orcid.org/0000-0002-1738-3381

RESUMEN

Laminas de Jengibre o Kion peruano fueron secados hasta aproximadamente una humedad en base húmeda de 10% usando un microondas domestico implementado con variador de potencia y lectura amperimétrica para el estudio de cinco niveles de potencia y cinco espesores de muestra de corte tipo lamina. Un delineamiento compuesto central rotacional (tipo estrella) fue usado para optimizar las condiciones de secado basados en el consumo de potencia eléctrica y espesor de la lamina de la muestra. Las condiciones óptimas se fijaron para los valores mínimos del tiempo de secado alcanzado. La aceptación global del producto mediante una prueba hedónica de nueve puntos fue realizada en los productos secos en cada ensayo. Se determinaron los parámetros de las condiciones óptimas que fueron de 800W y 3,5 mm de consumo de potencia y espesor de las láminas de jengibre respectivamente alcanzando un tiempo de secado de aproximadamente 8 min. Para el ajuste de los modelos matemáticos a los datos experimentales tanto para la curva de secado y de la isoterma de desorción, fue realizado el análisis de regresión no lineal, por el método de Simplex de Quasi Newton y se observó que con la ecuación de Midilli y la ecuación de G.A.B. representan el mejor ajuste a los datos experimentales para la curva de secado y desorción respectivamente.

Palabras clave: Secado por microondas; Jengibre; Metodología de superficie de respuesta; Isotermas.

ABSTRACT

Ginger or Peruvian Kion sheets were dried to approximately 10% humidity on a wet basis using a domestic microwave implemented with a power variator and amperometric reading for the study of five power levels and five sheet-type cut sample thicknesses. The response surface methodology through an experimental design of a star-type rotational central compound was used to optimize the drying conditions based on the consumption of electrical power and thickness of the sample sheet. The optimal conditions were set for the minimum values ​​of the drying time achieved. Overall product acceptance by a nine-point hedonic test was performed on dry products in each trial. The parameters of the optimal conditions were determined, which were 800W and 3,5mm of power consumption and thickness of the ginger slices, respectively, reaching a drying time of approximately 8min. For the adjustment of the mathematical models to the experimental data for both the drying curve and the desorption isotherm, the non-linear regression analysis was performed, by the Simplex method of Quasi Newton and it was observed that with the Midilli equation and the GAB equation represent the best fit to the experimental data for the drying and desorption curve respectively.

Keywords: Microwave drying; gengibre; Response surface methodology; Isotherm.

1. Introducción

El Jengibre es conocido como el Kion peruano, es un tallo subterráneo o rizoma de planta. Muy utilizado en la industria alimentaria y culinaria como saborizante, crece en un clima tropical, tal como se presenta en la selva de la región de Junín-Perú. El Perú ha logrado ingresar al mercado norteamericano en la exportación de Jengibre, antes era exclusivo del mercado chino. Este año de 2020, el Perú ha logrado ubicarse en el tercer puesto a nivel mundial después de China y Tailandia. El producto es fundamen-talmente orgánico de excelente calidad y con un sabor mucho más intenso que los comer-cializados a nivel internacional. Es un producto reconocido como remedio natural y rico en antioxidantes y se le atribuyen beneficios medicinales como el fortalecimiento del sistema inmunológico y últimamente a nivel mundial su consumo se ha elevado en el escenario Pandémico de la COVID-19 (MINCETUR, 2019; FAO, 2018).

El secado es una operación unitaria que consiste en la eliminación parcial o total del agua en los alimentos. Diferentes tecnologías de secado se vienen desarrollando con la finalidad de obtener productos de alta calidad considerando la optimización del proceso en relación a los costos de inversión y energía. Los métodos de secado controlados han conseguidos ventajas en relación al valor tecnológico, nutricional e inocuidad del producto (Muller & Heindl, 2006; Tomaino et al., 2005; Díaz-Maroto et al., 2003; Al Maiman et al., 2021). En las últimas dos décadas, el secado por microondas se viene utilizando para secar una variedad de productos alimenticios, evidenciándose como una buena técnica en la reducción del tiempo de proceso, costes operativos, en una mejora en la calidad del producto y disminución del impacto ambiental (Evin, 2011; Wang & Sheng 2006; Mujundar & Law, 2010).

La isoterma de sorción básicamente consiste en una representación gráfica del contenido de humedad de equilibrio en base seca versus la actividad de agua y es un parámetro muy importante en la industria para el diseño y optimización de procesos industriales, almacenamiento y envasado de alimentos (Labuza & Altunakar, 2007). Es la forma más frecuente presentada en la mayoría de los artículos científicos para datas de condiciones de equilibrio. Existen un sinnúmero de ecuaciones disponibles en la literatura para describir la isoterma de sorción, para este proyecto fueron usados modelos cinéticos basados en la monocapa (Modelo de BET), modelo cinético basado en la multicapa y condensación de película (modelo de GAB), otros modelos empíricos como el de Oswin-modificado y Smith y finalmente el modelo semiempírico de Henderson. El modelo GAB se considera el modelo de sorción más versátil disponible en la literatura y ha sido adoptado por un grupo de investigadores de alimentos de Europa occidental COST 90 (Martínez et al., 1998; Lewick, 1997; Wolf et al., 1984).

Metodología de Superficie de Respuesta es un conjunto de técnicas matemáticas utilizadas en el tratamiento de problemas en los que una respuesta de interés está influenciada por varios factores de carácter cuantitativo. El propósito inicial de estas técnicas es diseñar un experimento que proporcione valores razonables de la variable de respuesta y luego determinar el modelo matemático que mejor ajusta a los datos experimentales obtenidos. El objetivo final es establecer los valores de los factores que optimizan el valor de la variable de respuesta (Box et al., 2006; Jiju, 2014).

El objetivo de la investigación fue determinar experimentalmente los parámetros de las condiciones óptimas de secado de láminas de Jengibre con microondas y la aceptación global del producto usando la metodología de superficie de respuesta (RSM). Estudiar los datos de equilibrio del vapor de desorción del agua a diferentes humedades relativas y temperaturas. Y ajustar los datos experimentales a los modelos matemáticos disponibles en la literatura que describa los procesos del producto.

2. Material y métodos

2.1 El secador del laboratorio

Los experimentos de secado fueron realizados con un microondas modificado e implementado con un variador de tensión y lectura amperimétrica de intensidad de corriente instalado en el laboratorio de Ingeniería de Procesos y Operaciones Unitarias de la Facultad de Ingeniería Pesquera y de Alimentos de la Universidad Nacional del Callao.

2.2 Preparación y secado de las muestras

El Jengibre de la variedad amarilla, fue comprada en un mercado local y usada en todos los experimentos. En la realización de todos los ensayos de secado con el microondas se mantuvo constante la densidad de carga del producto que fue de 8,30 kg/m2 y el contenido promedio de la humedad del Jengibre fue de 84 ± 0,5% y de 83,5 ± 0,5% en base húmeda, en estado fresco y blanqueado respectivamente, que se determinó usando una estufa a vacío siguiendo el procedimiento de AOAC (2019). Las determinaciones de las diferentes potencias fueron obtenidas mediante un variador de tensión y con lectura de la intensidad de corriente. Durante el secado, las láminas de Jengibre fueron secadas en simple capa y pesadas periódicamente en una balanza digital semi-analítica hasta alcanzar la humedad final de aproximadamente 10% de humedad en base húmeda (aprox. 0,11 kgH2O/kgss en base seca). Se levantaron las curvas de secado representando la variación de la humedad en base seca versus el tiempo de secado.

2.3 Planeamiento experimental y análisis estadístico para la superficie de respuesta

Se diseñó un planeamiento experimental de compuesto central, que consiste en un planeamiento factorial completo 22, 4 puntos axiales (niveles ± 1,41) y cuatro puntos centrales (nivel 0), Tabla 1, totalizando 12 ensayos, realizados por duplicado y en forma aleatoria, para estimar los principales efectos de la potencia del microondas (500 – 1300 W) y espesor de la lámina de Jengibre (2 - 5mm) sobre el tiempo de secado y aceptación global del producto. Determinándose la condición optima de un adecuado menor tiempo de secado y de la aceptación global del producto.

En total fueron realizados 24 ensayos. Cada factor fue estudiado en cinco niveles diferentes, el planeamiento con los niveles codificados y reales es presentado en la Tabla 2. Para el análisis de los datos experimentales del planeamiento experimental se usó el programa de Statistica versión 12,0.  El siguiente modelo polinomial se ajustó a los datos:

Para el análisis de aceptación global, se contó con un grupo de 25 personas (10 hombres y 15 mujeres) estudiantes del área de alimentos. La evaluación fue realizada con un formato de la escala hedónica de 9 puntos, usando valores numéricos equivalentes a: 1 “deguste extrema-mente”, 2 “deguste mucho”, 3 “deguste modera-damente”, 4 “deguste ligeramente”, 5 “no guste ni deguste”, 6 “guste ligeramente” 7 “guste moderadamente” 8 “guste mucho” y 9 “guste extremamente”.

2.4 Modelamiento matemático para las curvas de secado

Los modelos matemáticos caracterizan las curvas y velocidades de secado de diferentes materiales biológicos y que se encuentran ampliamente disponibles en la literatura. Las curvas de secado fueron ajustadas con cuatro modelos matemáticos usados con alta frecuencia en experiencias de secado de productos agroindustriales, La ecuación de Newton, es una ecuación simplificada de la solución generalizada de series de la segunda ley de Fick (Doymaz, 2011; Goneli, 2014). El modelo de Page es un modelo matemático empírico de tipo exponen-cial, que ha tenido mucho éxito en diferentes experiencias de secado de productos agroindus-triales (Minaei et al., 2012; Wang et al., 2007, Toğrul & Pehlivan, 2003), El modelo de Henderson-Pabis, que involucra tres constantes y finalmente el Modelo matemático empírico de Midilli que involucra 4 constantes de secado, en la Tabla 3, se presenta los modelos usados para simular la curva y cinética de secado.

2.5 Determinación de la Isoterma de desorción

Las condiciones de equilibrio y obtener las isotermas de desorción, se utilizaron sales seleccionadas que promueven ambientes con diferentes humedades relativas en su interior (Greenspan, 1977; Kitic et al., 1986), envases de vidrio de 200 ml de capacidad con tapas Twist-off y balanza analítica. Para la evaluación de las isotermas de desorción del Jengibre, las muestras fueron previamente escaldadas a 90 ºC por 5 min, fueron obtenidas usando aproximada-mente 4,5 g cortados en forma de cubos de 2x2x2 mm (con el objetivo de mejorar el fenómeno de transferencia de masa). Previamente se prepararon pequeños depósitos de papel de aluminio acondicionados dentro de cada capsula y éstos con las muestras. Posteriormente fueron colocados en envases de vidrio herméticamente cerrados con las soluciones de sales recomendadas por el proyecto COST-90 (Bertuzzi et al., 2003). Los ensayos fueron realizados por triplicado y acondicionados los envases de vidrio para mantener las capsulas sobre la superficie libre de las sales saturadas. Las isotermas de desorción fueron construidas para las siguientes temperaturas: 20, 40 y 60 ºC. Fueron realizadas usando la técnica gravimétrica mediante el método estático con registro discontinuo de variación de peso.

Tabla 3

Modelos matemáticos usados para ajustar a los datos experimentales del secado de láminas de Jengibre

X(t) es el contenido de humedad en base seca del producto en el tiempo (t) de secado; Xe es el contenido de humedad de equilibrio en base seca; ki y n son las constantes de secado en los modelos y t es el tiempo de secado.

2.6 Modelamiento matemático de las isotermas de desorción

En la tabla 4 se presentan los modelos matemáticos de las isotermas usadas en esta investigación, en relación a las ecuaciones de BET y GAB, las constantes Xm, C y K, dependen de la temperatura y características del producto. La ecuación de Oswin fue modificada incluyendo las constantes A y B que depende de la temperatura “t” siendo la constante C una característica del producto. Las constantes A y B son las constantes de la ecuación para los modelos de Smith y Henderson respectivamente. La variable aW es la actividad de agua o la humedad relativa generada por las sales saturadas en la atmosfera interna del recipiente.

2.7 Análisis de los datos para la curva de secado e isoterma de desorción

Para el ajuste de los modelos matemáticos a los datos experimentales se hizo uso de Solver de Excel 2010, se realizó el análisis de regresión no lineal por el método de Simplex de Quasi Newton, con una precisión del orden 10-6, siendo la celda objetivo el estadístico del error cuadrático medio (MSE: Mean Square Error), ecuac. 11:

3. Resultados y discusión

3.1 Análisis de la superficie de respuesta del tiempo de secado y Aceptación global de las láminas secas de Jengibre

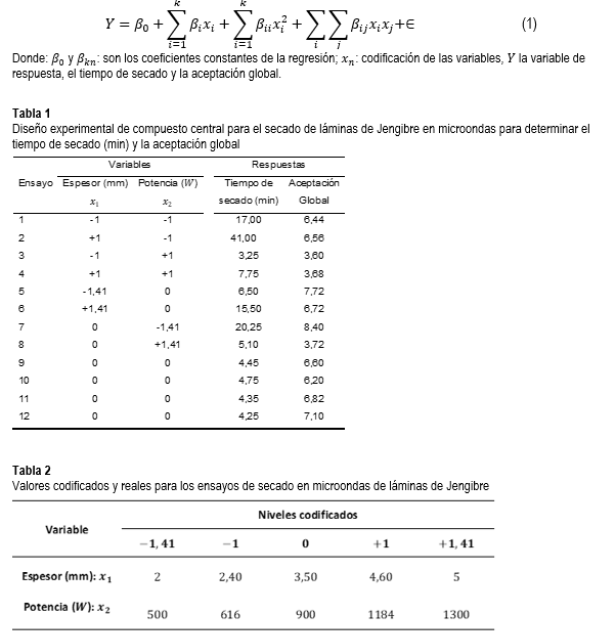
Para el análisis de la superficie de respuesta se consideró estadísticamente el Error Puro, en la Figura 1 se presenta el análisis de los efectos sobre la variable de respuesta del tiempo de secado, observándose una fuerte interacción de las variables (p < 0,05). Se evidencia que la variable de espesor de la lámina de Jengibre tiene efecto directamente lineal y cuadrático sobre el tiempo de secado; la variable potencia tiene un efecto lineal de efecto negativo al tiempo de secado y en forma cuadrática es directamente proporcional. Siendo la interacción negativa de estas variables sobre el tiempo de secado.

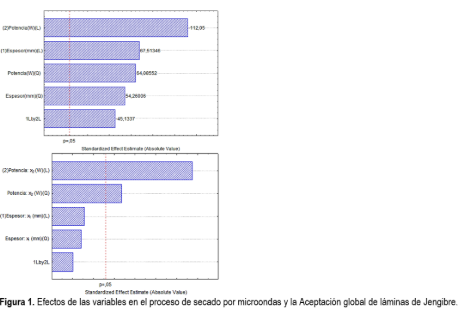
Los modelos matemáticos que se generaron para obtener la superficie de respuesta para ambas variables son estadísticamente válidos (p < 0,05).

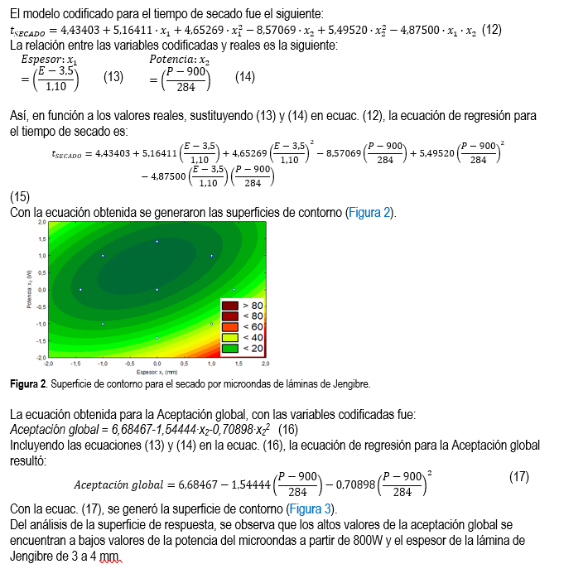
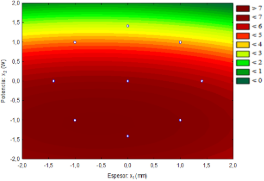
Figura 3. Superficie de respuesta para la Aceptación global del producto seco de láminas de Jengibre secado por microondas.

Los puntos óptimos para alcanzar los valores mínimos de secado por microondas para el planeamiento experimental propuesto se encuen-tran bastante cerca y en el intervalo que corresponde a los puntos centrales del planea-miento experimental, para la potencia que varía en la faja de 800 a 1300 W y el espesor de la lámina de Jengibre entre 2,40 a 4,0 mm.  Seguidamente se realizaron tres pruebas de secado usando tres potencias: 800, 1030 y 1300 W, manteniendo un solo espesor de lámina de Jengibre de 3,5 mm. Fue sometido al análisis de Aceptación global (Figura 4), cuyos resultados del análisis de varianza para los tres grupos, a un nivel de confianza del 95% el valor medio de la aceptación global no es significativamente diferentes (p > 0,05).

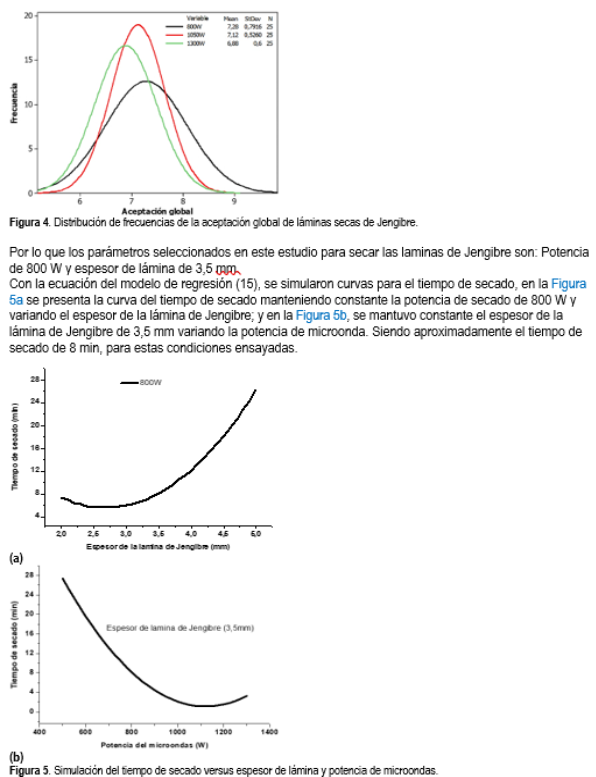
3.2 Análisis de la curva y velocidad de secado

Para estas condiciones se establecieron las curvas de secado y el respectivo modelamiento matemático (Tabla 5). La curva de secado muestra un proceso de disminución del contenido de humedad versus el tiempo de secado de manera netamente decreciente hasta obtener la humedad final del 10% en base húmeda (0,106 kgH2O/kgss en base seca).

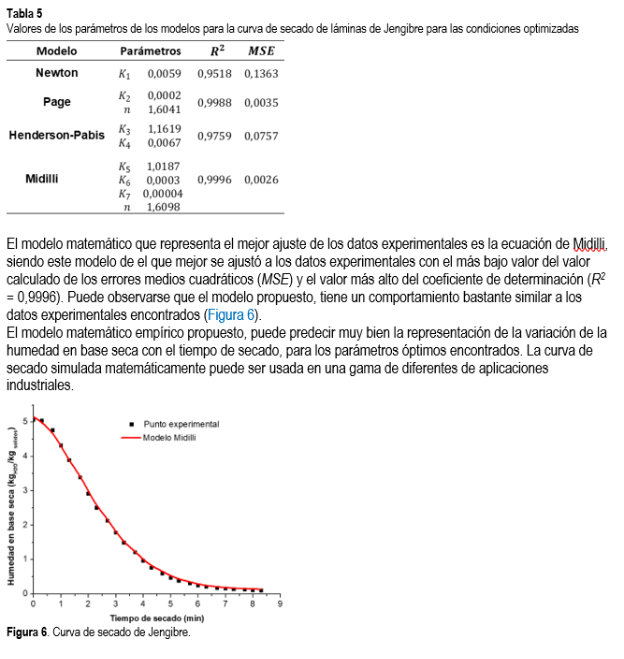
En la curva de la cinética de secado (Figura 7a) se obtuvo usando los valores numéricos de la curva de secado simulada con la ecuac. de Midilli de la variación de la humedad en base seca con el tiempo, observándose una elevación de la velocidad de secado (Figura 7b) en los primeros dos minutos (dX/dt)max de 1,30 kgH2O/kgss. min) para luego caer en forma sostenida hasta el 4 min 30 s, y luego ir variando más lentamente la velocidad de secado hasta la humedad final. Las curvas de secado de la humedad promedio X(t) versus el tiempo de secado de las condiciones óptimas de secado de las láminas de jengibre, fueron realizadas y ajustadas sobre la base estadística del cálculo del error medio cuadrático (MSE: Mean Square Error) y el coeficiente de determinación (R2).

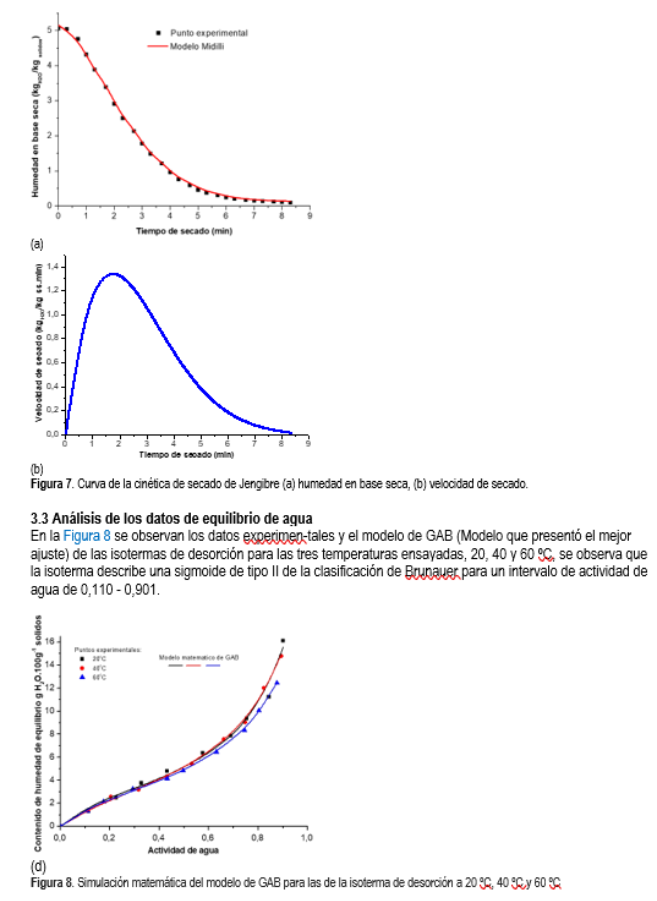
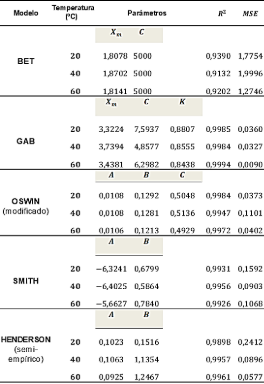
En la Tabla 6 se resumen los valores de los parámetros de los modelos para las tempe-raturas de 20, 40 y 60 ºC respectivamente. Un alto valor del coeficiente de determinación R2 y un bajo valor de MSE, confirman el buen ajuste de los datos experimentales por los cinco modelos. La ecuación de GAB presentó el mejor ajuste a los datos experimentales para las tres temperaturas ensayadas, lo que reafirma la recomendación dada por el proyecto COST 90.

Tabla 6

Valores de los parámetros de los modelos matemáticos de la isoterma de desorción para las láminas de Jengibre

4. Conclusiones

El secado de láminas de Jengibre fue estudiado en un microondas implementado a escala de laboratorio, en un intervalo de Potencia de 500-1300 W y espesor de lámina de Jengibre de 2-5mm. En relación a la aceptación global del producto seco se determino que en las condiciones de 800 W de potencia y 3,5 mm de espesor de lámina de la muestra se obtuvo un mejor resultado, siendo el tiempo de secado de aproximadamente 8 min. La curva de secado mostró una sola etapa de secado decreciente siendo que a los 2 minutos del proceso de secado la velocidad de secado mostro un máximo valor de aproximadamente 1,30 kgH2O/kgss min. Se usaron 4 modelos para describir la curva de secado, siendo el modelo de Midilli, que mostró el mejor ajuste que compara-do con los otros modelos inclusive el de Page. El estudio de los datos de equilibrio determinó una isoterma de desorción de tipo II, que fue muy bien simulada por la ecuación de GAB.

Agradecimientos

Los estudios fueron conducidos gracias al apoyo del Laboratorio de Ingeniería de Procesos y Operaciones Unitarias (LIPOU-FIPA) de la Facultad de Ingeniería Pesquera y de Alimentos de la Universidad Nacional del Callao, Provincia Constitucional del Callao, Lima, Perú.

Referencias bibliográficas 

AOAC. (2019). Oficial Methods of Analysis (21st Edition, W. Horowitz, ed.). Association of Official Analytical Chemist. Washington, DC.

Bertuzzi, M., Armanda, M., & Gottifredi, J. (2003). Thermodinamic Analysis of Water Vapour Sorption of Edible Starch Based Films, Food Sci Tech Int., 9(2), 115-121.

Box, G., Hunter, J., & Hunter, W. (2005). Statistcs for experimenters: Design, Innovation, and Discovery. 2nd Edition, Jhon Wiley & Son ed., New York.

Díaz-Maroto, M. C., Pérez-Coello, M. S., & Cabezudo M. D. (2002) Effects of different drying methods on the volatile components of parsley (Petroselinum crispum L.). European Food Research and Technology, 215(3), 227-230.

Doymaz, I. (2011). Drying of thyme (Thymus vulgaris L.) and selection of a suitable thin-layer drying Model. Journal of Food Processing and Preservation, 35(4), 458-465.

Evin, D. (2011) Microwave drying and moisture diffusivity of white mulberry: experimental and mathematical modeling. J Mech Sci Technol, 25, 2711.

FAO. (2018). World Food and Agricultural-Statistical Poketbook. Rome 254 pp. Licence: BY-NC-SA 3,0 IGO.

Goneli, A. L. D., Vieira, M. D., Vilhasanti, H. C. B., & Gonçalves, A. A. (2014b) Mathematical modeling and effective diffusivity of mastic leaves during drying. Tropical Agricultural Research, 44(1), 56-64.

Greenspan, L. (1977). Humidity fixed points of binary satured aqueous solutions. J. Res. National Bureu Standards. A. Phys & Chem, 81(1), 89-96.

Jiju, A. (2014). Design of Experiments for Engineers and Scientists (Second Edition), pp 7-17, Published by Elsevier Ltd.

Kitic, D., Jardim, D., Favetto, G., Resnik, S., & Chirife, J. (1986) Theoretical prediction of the water activity of saturated salt sodium´s at various temperatures. Journal of Food Science, 51(4), 1037-1041.

Labuza, T. P., & Altunakar, B. (2007). Water prediction and moisture sorption isotherms. In Water Activity in Food, Pp: 109-154, IFT Press, Blackwell Pu.

Minaei, S., Motevali, A., Ahmadi, E., & Azizi, M. H. (2012) Mathematical Models of Drying Pomegranate Arils in Vacuum and Microwave Dryers. J. Agr. Sci. Tech., 14, 311-325.

Ministerio de Comercio Exterior y Turismo. MINCETUR. (2021). Envíos de fruta y jengibre mantienen al alza agro exportaciones no tradicionales; Abril/2021.

Muller, J., & Heindl, A. (2006). Chapter 17: Drying of Medicinal Plants. Medicinal and aromatic plants - agricultural, commercial, ecological, legal, pharmacological and social aspects, Publisher: Springer, Editors: Bogers, R J Craker, L E Lange Pp: 237-252. Printed in the Netherlands.

Al Maiman, S., Nawal, A. A., Almusallam, I. A., Jawad, M., Alsuliam, S., Osman, M. A., & Hassan, A. B. (2021) The Potential of Exploiting Economical Solar Dryers in Food Preservation: Storability, Physicochemical Properties, and Antioxidant Capacity of Solar-Dried Tomato (Solanum lycopersicum) Fruits. Foods, 10, 734.

Toğrul, İ. T., & Pehlivan, D. (2003). Modeling of drying kinetics of single apricot. Journal of Food Engineering, 58(1), 23–32. 

Tomaino, A., Cimino, F., Zimbalatti, V., Venuti, V., Sulfaro, V., De Pasquale, A., et al. (2005). Influence of heating on antioxidant activity and the chemical composition of some spice essential oils. Food Chemistry, 89, 549–554.

Wang, J., & Sheng, K. (2006). Far-infrared and microwave drying of peach. LWT - Food Science and Technology, 39(3), 247-255.

Wang, Z., Sun, J., Chen, F., Liao, X., & Hu, X. (2007). Mathematical Modeling on Thin Layer Microwave Drying of Apple Pomace with and without Hot Air Predrying. Journal of Food Engineering, 80, 536–544.

Wolf, W., Spies, W. E. L., Jung, G., Weisser, H., Bizot, H. & Duckworth, R. B. (1984). The water-vapour sorption isotherms of microcrystallime cellulose and purified potato starch. Results of collaborative study. Journal of Food Engineering, 3, 51-73.